Kinematic mapping trajectory estimation

Integrated trajectory estimation for 3D kinematic mapping with GNSS, INS and imaging sensors: A framework and review¹

方法分类

1. 多步方法。

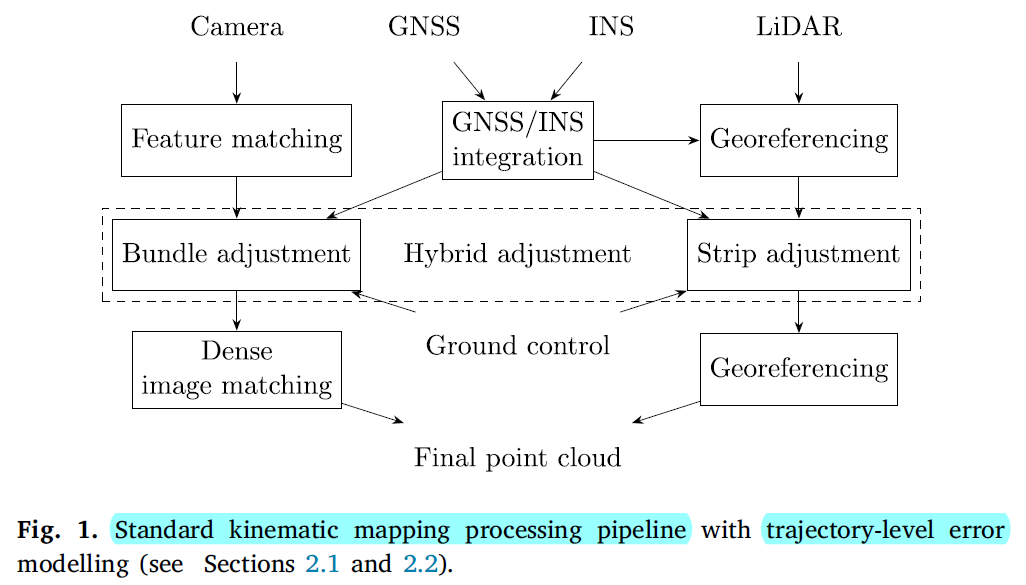
​ 流程：首先用Kalman filtering 将GNSS和IMU融合到一起，如果轨迹足够准确，可以直接获得3D点云。也可以在后面加一个平差步骤，结合影像传感器的观测实现融合传感器定向，目的是：1）改正轨迹；2）传感器定向和标定；3）获取3D模型数据，e.g.点云。

​ 需要有一些假设：通常假设轨迹误差是由于缓慢变化的 GNSS 误差或未补偿的惯性传感器漂移造成的，因此是低频的，而轨迹的较高频率分量相对准确。 实际上，校正要么与飞行几何相关联，作为每条带的固定偏移，要么建模为缓慢时变。 由于轨迹误差在带内也可能变化很大，因此这种调整在实践中通常需要高度灵活的校正模型，而这也是的模型有较高的过拟合风险，导致点云中出现全局的变形。

​ 这些问题是的在传感器层级进行统一的误差建模的方法开始流形。

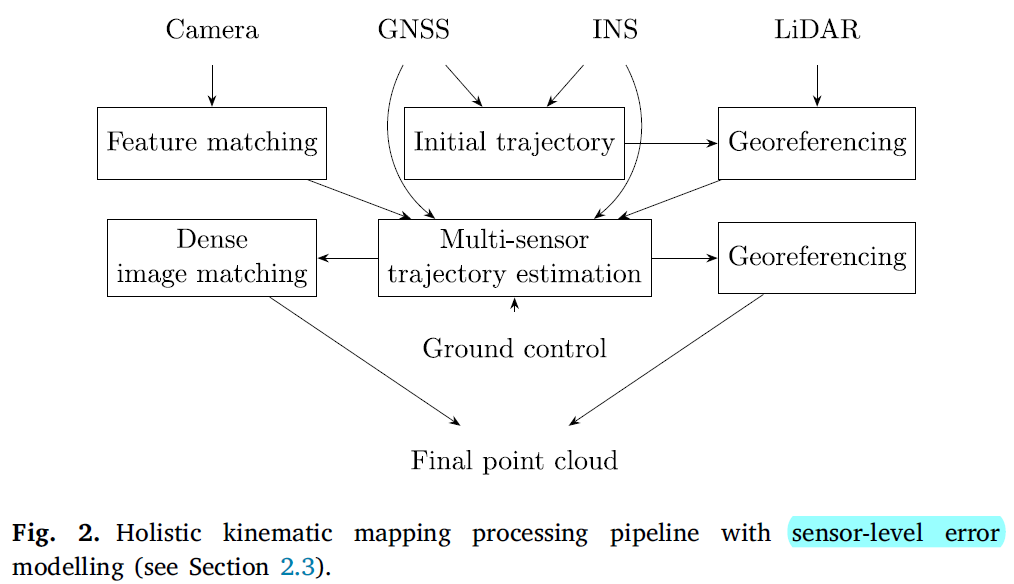
2. 联合方法。

​ 主要流行于多传感器融合。

​ 值得注意的是，根据最终应用的不同，对平台轨迹的要求也存在一些差异。 出于导航目的，例如汽车导航或机器导航，人们通常对平滑的车辆轨迹感兴趣。 对于测量，即传感器测量的地理配准，感兴趣的轨迹是成像传感器本身的轨迹，它可能相对于车架是刚性的，也可能不是刚性的。 为此，任何振动都不应被视为噪声，因此不会被滤除，因为这些振动确实会影响测量。 同样，地理配准的精度要求也很高。 标称激光测距精度约为 2 厘米，但据报道，对于足够平坦的地形，毫米范围内的偏差已被报道。 因此，轨迹精度通常是限制因素。 由于机载遥感的高测量范围，方向误差（无论是轨迹误差还是扫描仪和 INS 之间的未对准）占主导地位。

​ 可以按照耦合方式进行划分：

​ 松耦合是指轨迹级别的误差建模：来自不同传感器的位置和/或方向估计被组合成一个综合轨迹估计。 以损失部分信息换来计算效率的提升，实现复杂度相较于紧耦合是比较小的。

​ 紧耦合是指误差在传感器级别建模； 即测量以原始形式组合，并且只产生一个轨迹估计。

-	-

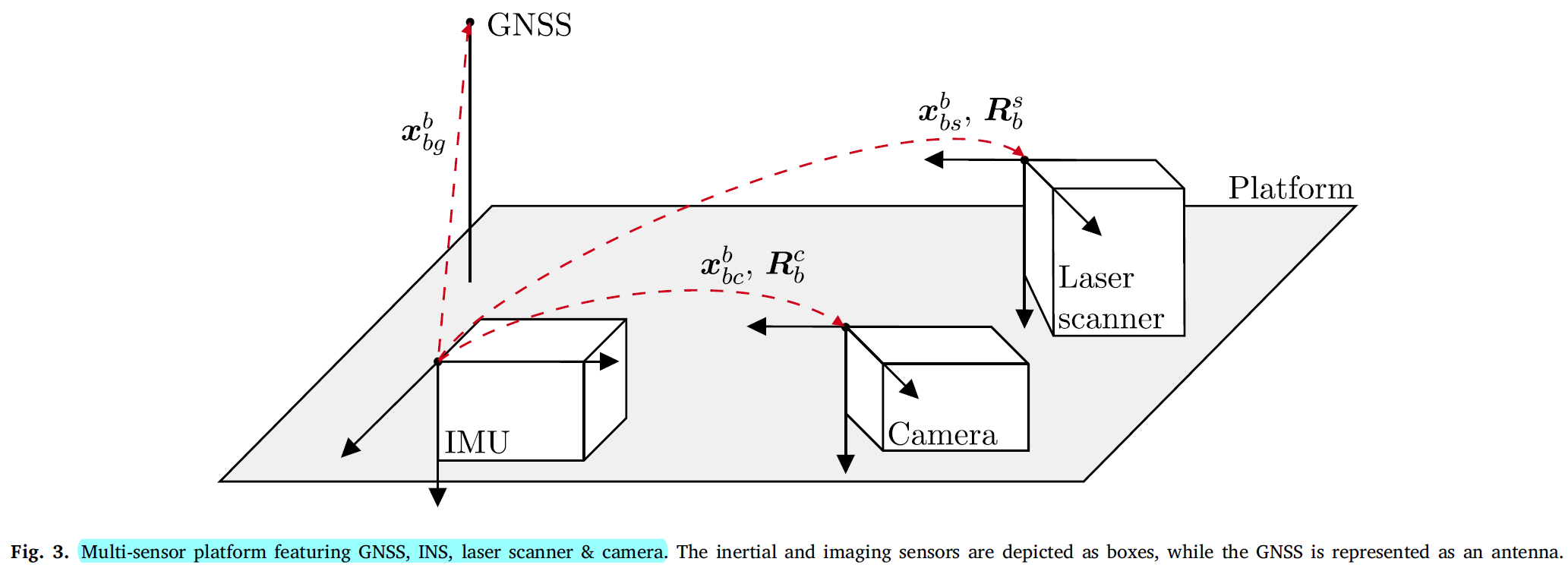
Multi-sensor platform

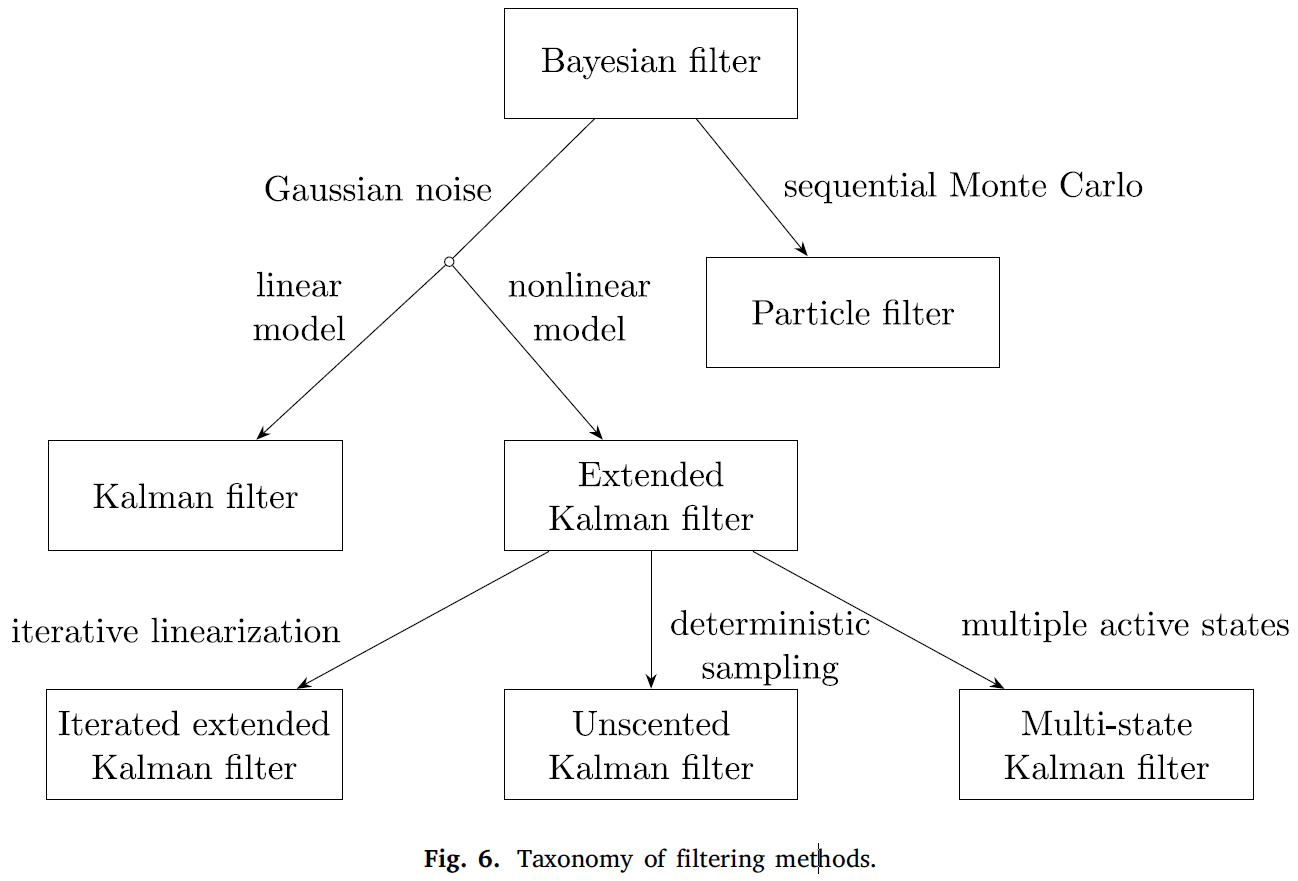
Taxonomy of filtering methods.

在Kalman filter下面还可以加一个error state kalman filter。

建模框架

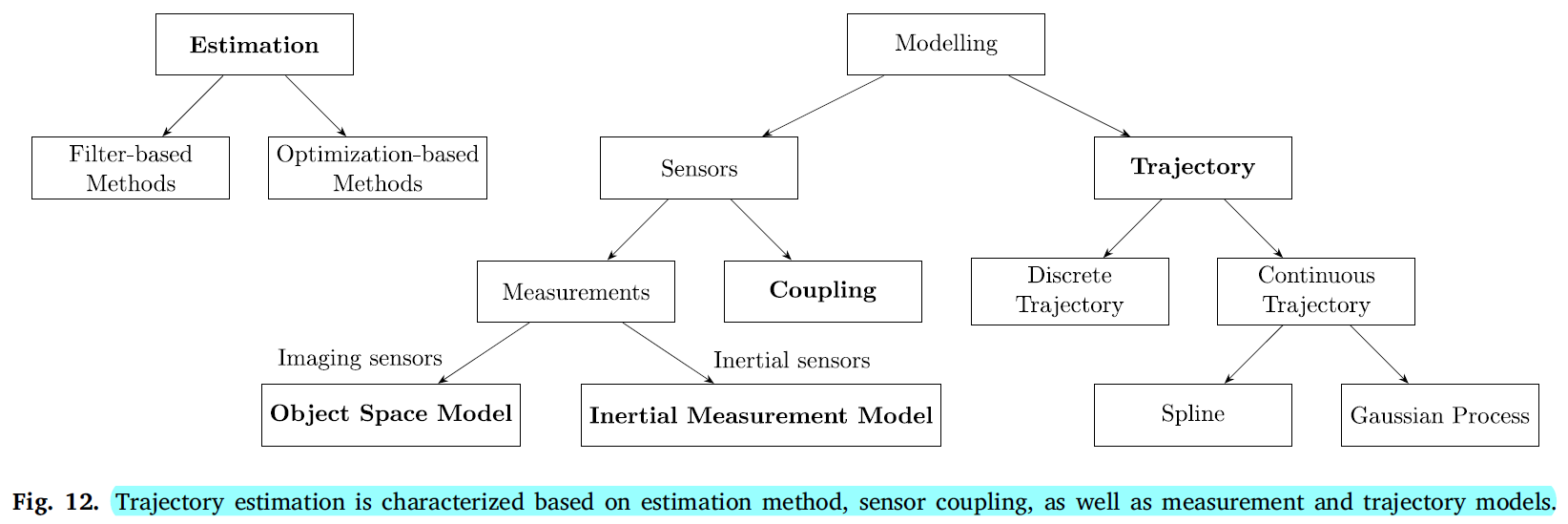
​ 轨迹估计需要对两个有些不同的方面进行建模：传感器测量的建模和轨迹本身的建模。 虽然经典方法将轨迹（以及其他时变量）表示为状态变量的离散时间序列，但一些较新的公式使用连续表示。

​ 通常，有必要在成像传感器采样时间获得轨迹估计。 如果此类测量的数量很大，则可能无法在所有这些时间明确估计轨迹，要求轨迹可以以某种方式由相对较少数量的参数表示，有两种方案：1）计算固定时间点的轨迹估计，并使用插值法得出所需的中间值，或2）使用可在需要时进行评估的显式连续时间表示。

文献总结

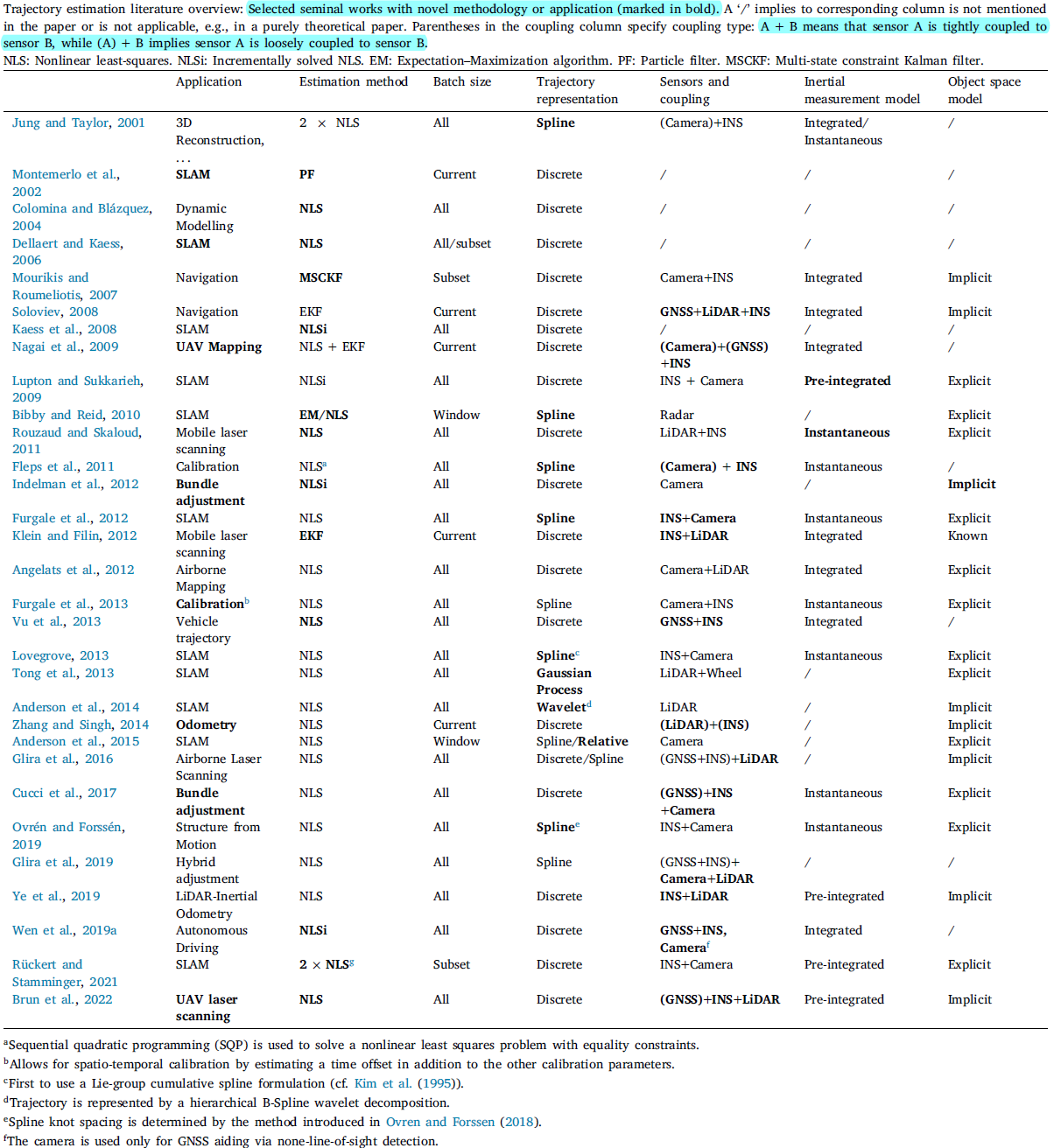
​ 这个Tong 2013²中做了基于高斯过程的状态估计，Furgale 2012³-2013做了基于Spline的状态估计。但是两种方法之间的区别和联系，以及又是是什么，尚不明确。Furgale使用的B-Spline的表示方法是Qin的方案。高斯过程的方案需要对运动有一个先验，一般使用的都是高斯白噪声。这样才能得到可逆的协方差矩阵，提升计算效率。

• 连续轨迹表示在减少参数数量和轨迹保真度之间进行权衡。 这种权衡通常会导致更高频率的平滑，这可能是理想的，也可能不是理想的，具体取决于应用。

讨论

趋势

• From recursive filtering to batch optimization：组合导航的解决方案以前基于递归估计，即卡尔曼滤波器类型的解决方案。 最近，基于批量 MAP 估计的方法越来越受欢迎。 存在增量或简化的解决方案，但主要是出于性能原因：尽管计算量大，但理论上更可取全批量处理方法。
• From discrete to continuous trajectory representations：经典的过滤方法将位置和方向的演变参数化为一组离散的状态。 由于包含多个可能异步采样的传感器需要以非常高的频率估计位置和方向，因此连续轨迹参数化已被证明是有用的并且被广泛使用，尤其是在机器人社区中。 这允许在任意时间评估位置和方向。 除了随机先验之外，还可以通过选择合适的轨迹表示来合并关于轨迹的额外“确定性”先验信息。 另一方面，如果测量是同步的或线性插值就足够了，则连续公式的计算要求可能更高。 应该提到的是，迄今为止还没有对所有不同的轨迹表示进行详尽的比较。
• From trajectory level to sensor level error modelling：轨迹级误差建模对于小误差或遵循某些特征的误差是有效的。 然而，这种方法可能导致轨迹变形，随后导致 3D 模型变形，因为忽略了基础测量（GNSS 和 IMU）。 估计算法的进步以及可用的计算能力导致了整体多传感器估计方法的趋势，其中误差在传感器级别建模，即以紧密耦合的方式。
• Towards mathematically rigorous modelling：最近提出的方法采用了更复杂的数学技术。 这以不同的方式表现出来：对于轨迹表示，越来越多的经典欧拉角表示受到批评，并被尊重底层李群结构的参数化方法所取代。 以前，加权最小二乘法只是作为一种优化工具使用，但现在它主要用于概率框架内，因为对准确随机误差建模的需求变得更加明显。 对于这些统计解释，所做的工作是为了合并具有不同的、可能是先验未知概率密度的误差。 在计算可行的情况下，首选提供强大理论保证的估计器，无论是关于统计最优性还是数值性能。

挑战

​ 从纯理论的角度来看，紧耦合的全批量估计没有缺点，其中同时考虑所有测量。 与增量或松散耦合的方法相比，可以预期紧密耦合的全局方法在鲁棒性和准确性方面表现更好。 然而，这种“完全紧耦合”方法的实用公式已被证明是难以捉摸的。 在大多数情况下，进行简化以允许更有效的处理，或者传感器以松散的方式部分耦合以简化模型和必要的计算。 在各种简化和不同的耦合组合中，还没有建立明显优越的方法。 如果趋势是存在的，并且全局紧耦合是优越的，那么为什么在实践中没有体现出来呢？ 我们认为这主要是由于两个原因，概述如下:

• Model complexity：虽然采用更紧密耦合的方法在实践中通常表现出更高的性能，但它需要付出巨大的努力。 对于传感器级误差建模，需要深入了解传感器才能准确地对误差建模，而不会在估计中引入系统误差。 为此，必须访问原始传感器数据。 这对于受到出口限制并且通常不允许访问原始数据而仅提供集成导航解决方案的高质量 IMU 来说尤其如此。 然而，对于 GNSS 数据，这个问题已经解决了：RINEX 提供了一种标准化的、文档化的数据交换格式。 然而，紧耦合需要同时估计所有相关参数和测量值。 与松散耦合相比，这导致更高的处理和内存要求。 更高效、可并行化的算法和更快的硬件将使进一步利用紧密的传感器耦合成为可能。
• Lack of comparative studies：上述所有方法都经过实验评估，但针对不同的传感器模式和应用，并且主要是基于个体，这些都没有比较过。 Cioffi 针对不同的机器人场景将离散时间和基于样条的 SLAM 实现进行了比较。 然而，不同方法之间的一般深入比较是困难的，一方面是由于缺乏高精度参考数据，另一方面是因为很少有实现是公开可用的，并且由于模型的复杂性而不会经常进行重新实现。 第 5 节中介绍的文献中提供了不同方法的示例应用，特别是不同轨迹表示的示例应用。在一些研究中，低级和高级硬件的组合用于测试关于参考轨迹的新方法 更好的系统。 然而，评估更好系统的问题仍然存在。 任何比较也必然限于特定用例：对轨迹解决方案的要求，以及对平台动力学、振动和传感器噪声等系统行为的假设，因应用而异。 对于移动激光扫描，尤其是在城市环境中，由于 GNSS 接收不良或多径效应导致的定位误差起着很大的作用。 对于机载应用，GNSS 通常没有问题，但需要高精度定位，因为由于测量范围较长，定位误差对地理参考数据有很大影响。
• Challenges for kinematic mapping applications：运动学映射应用中普遍的高精度和准确度要求提出了进一步的挑战。 尽管在这方面已经做了大量工作来提高低成本传感器的精度，但许多测量应用程序仍然依赖于昂贵的高级硬件。 由于需要对各种算法组件进行微调，可用的处理解决方案需要经验丰富的操作员。 其他基于部分处理工作流程的商业黑盒解决方案，这些解决方案在报告的准确性方面往往过于乐观。

展望

​ 总而言之，许多不同领域的贡献取得了很大进展。 几个明显的趋势已经确立。 然而，== 最佳解决方案仍不清楚==。 因此，主要的挑战是允许对不同方法进行严格的评估和比较，这反过来又需要合适的基准数据。 未来在这个方向上的工作将允许开发更准确、可靠和自动的轨迹估计方法，这反过来有利于所有与运动学映射相关的活动。